大学編入の数学の対策方法とおすすめ参考書

こんにちは!ステップ編入学院の運営です!
この記事は、
大学編入の数学って難しいな。高校範囲の数学も苦手なのに大学範囲となったらさっぱりわからない…何かいい勉強法とか参考書とかあれば知りたいな。
という疑問にお答えします。
結論ですが大学編入の数学は出題される範囲が限定的でピンポイント対策すれば8割以上取ることが可能です。
8割取れれば編入試験に合格でき、他の教科に余裕ができるので記事内で掘り下げて説明します。
ちなみにこの記事を書いている僕は大学受験に失敗してFラン大学に進学。編入試験を知り人生を変えたい一心で努力し、大阪大学、神戸大学に合格しました。そういった経験から解説します。
〜本記事の内容〜
- 大学編入数学対策は2点だけ理解しておこう
- 編入数学の勉強方法3ステップ
この記事を読めば、「編入数学で8割とりたいけど何をすればいいかわからない」、「編入数学の勉強方法がわからない」といった疑問が無くなりますよ!
大学編入数学対策は簡単【8割取るために知っておきたいこと3ポイント】
編入数学の勉強を始める前にこの3ポイントを抑えておけばOK。
- 出題範囲が限定的
- 丸暗記でOK
- 参考書は「編入数学徹底研究」でOK
この3ポイントを理解してこの記事の通り勉強を進めれば、編入数学で8割以上取れるようになります。
出題範囲が限定的
大学編入数学の出題範囲はかなり限定的でほとんどの場合が、「微分・積分」と「線形代数」だけで対応可能です。

しかも「微分・積分」や「線形代数」を全て勉強する必要はなく、大学・学部によって更に出題される範囲は限定されます。
下記が「微分・積分」、「線形代数」を更に細かく分けたものになります。

- 微分・積分 ・・・ 微分法、不定積分、定積分、偏微分、重微分、微分方程式
- 線形代数 ・・・ 行列、行列式、ベクトル空間、線形写像、固有値、内積
例えばA大学では「微分・積分」が出題されるけど、「微分方程式」、「不定積分」しか出題されないので、他の「微分法」などは勉強する必要なし。という感じです。
だいたいどこの大学も「微分・積分」と「線形代数」が出題されるだけですが、大学によってはプラスαで下記のどれか1つが出題されます。
確率、複素解析、フーリエ解析、ラプラス変換、ベクトル解析
この通りです。
正直、上位の難関大学でなければプラスαでこのような出題をされることは少ないです。
しかも「微分・積分」、「線形代数」はおきまりの問題しか出題されません。
この事実がかなり重要で解き方さえ覚えてしまえば、どんな問題も解けてしまうということです。
なので試験科目に「数学」がある場合はラッキーだなと思うようにしましょう。
文系で経済学部を受験する人で数学に苦手意識がある人もいるかもしれませんが、慣れれば解ける問題がほとんどです。
諦めずに冷静に過去問を分析して出題される範囲を確認しましょう。
丸暗記でOK
そんな出題範囲が限定的な編入数学ですが、試験対策はずばり丸暗記です。
数学って丸暗記で大丈夫なの…?
と心配される方も多いかもですが大丈夫です。
さきほども話しましたが、大学編入数学はおきまりの問題。もっと言うとほぼ同じ問題が出題されます。
というのも数学には型が存在していまして、型通りに問題を解き進めれば解答に辿り着くことができます。通常難しい問題は、その型を組み合わせた応用問題が出題されるのですが、ほとんどの編入数学の問題は1つの型からできています。
大阪大学、神戸大学くらいまでのレベルならこの方法で8割は取ることができます。
残念ながら東京大学、京都大学は型を組み合わせた問題が出題されるのでこの方法は通用しません。
なので数学は解き方を暗記すべきです。
もちろん最低限の基礎理解は必要ですが、問題を見たときにこのようになっていれば完璧です。
- ①テスト問題確認
- ②行列の問題が出題されている
- ③勝手に手が動き出す
と行った感じまで持っていければ必ず8割は取れます。
そんな型を暗記する方法ですが、具体的に記事後半で紹介します。
参考書は「編入数学徹底研究」でOK
ステップ編入学院には「編入数学のおすすめ参考書」はありませんか?という質問をいただくのですが、上記の「編入数学徹底研究 頻出問題と過去問題の演習」をおすすめしています。
というか編入試験科目に数学がある人は、この参考書は必須なのですぐにポチりましょう。
実際に私もこの1冊をやり込み神戸大学工学部へ合格しました。
この1冊は編入数学に必要な知識が過去問ベースでコンパクトにまとまっているので、この1冊と過去問だけで数学対策はバッチリです。
さきほど紹介した通りで、出題範囲が限定的な編入数学を全てカバーしています。
微分・積分(微分法、不定積分、定積分、偏微分、重微分、微分方程式)、線形代数(行列、行列式、ベクトル空間、線形写像、固有値、内積)、確率、複素解析、フーリエ解析、ラプラス変換、ベクトル解析
章ごとに詳しく分れているので、志望校の過去問を確認して必要な項目だけ対策しましょう。
ただし注意点がありまして、「数学が極端に苦手」であったり、「独学が難しい」場合は1人でこの1冊を進めるのは厳しいと思います。
ステップ編入学院では数学専門の教師が丁寧に解説・指導を行っていますので、興味のある方は体験授業を受講してみてください。
ちなみにECC編入学院の数学の講師はこの参考書の筆者でして、講座はこの参考書ベースで行われていました。この参考書を買うだけでその講座と同程度の内容が得られると考えればお得ですよね。
またよく受験生の方から、
この参考書の応用問題バージョンの「編入数学過去問特訓: 入試問題による徹底演習」はやるべきですか?
といった質問をされるのですが、やる必要なしです。
こちらの参考書ですね。
理由は単純でこの参考書をやれば8割から10割まで点数を上げることが可能なのですが、編入試験は8割取れればOKで、8割から10割まで上げるために時間を使うのが勿体ないからです。
「時間的に余裕がある人」、「東京大学、京都大学、その他理学部の数学科などを受験する人」はやってみる価値があるかもしれませんが、ほとんどの受験生は1つ目の「編入数学徹底研究 頻出問題と過去問題の演習」だけで大丈夫です。
編入数学の勉強方法3ステップ
数学は暗記して、「編入数学徹底研究 頻出問題と過去問題の演習」で勉強すれば大丈夫なんだなと漠然と理解していただけたかなと思います。
ここから具体的な編入数学の勉強方法を紹介します。
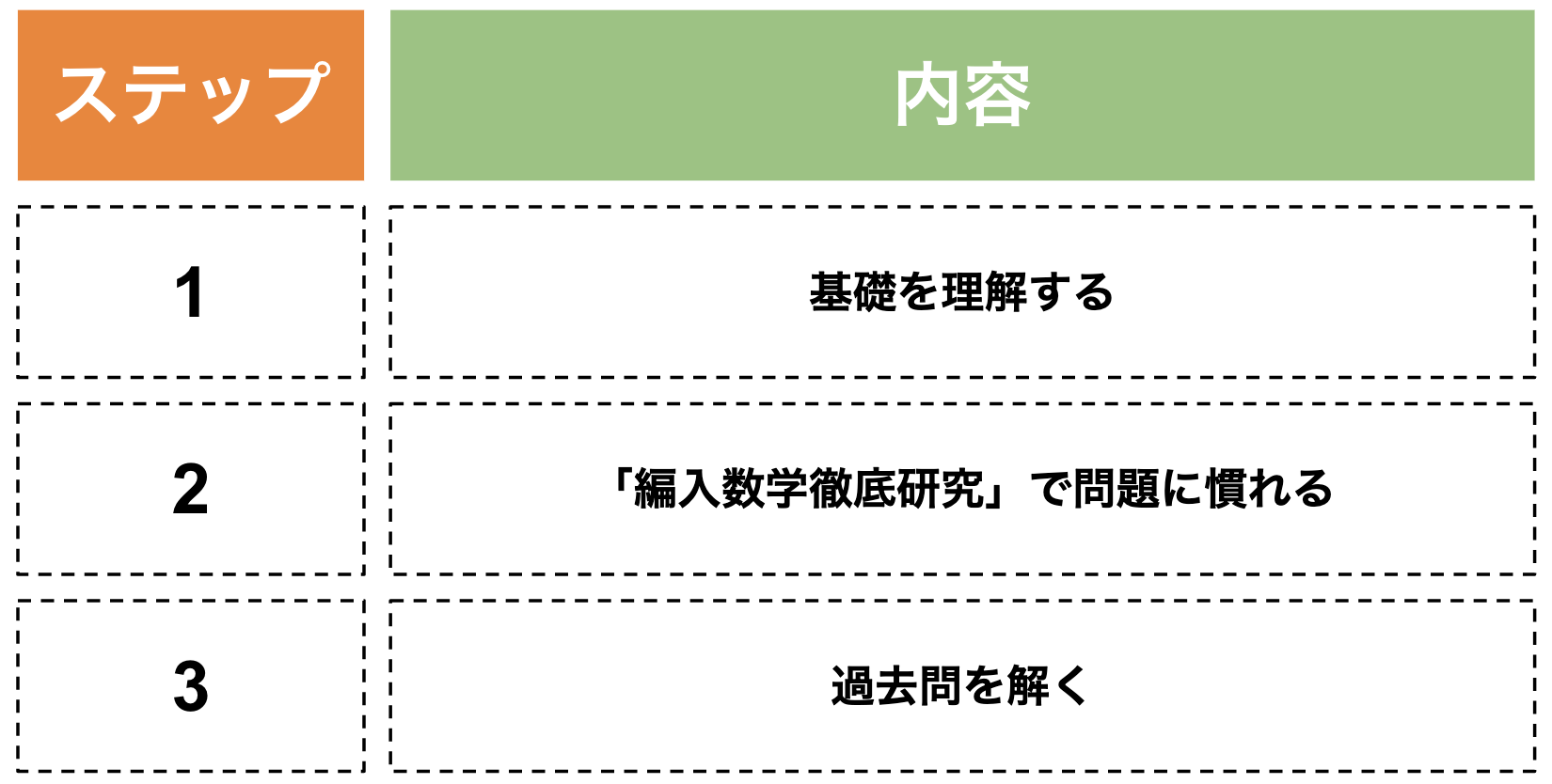
基本的に下記の3ステップで進めます。
- ステップ1. 基礎を理解する
- ステップ2. 「編入数学徹底研究」で問題に慣れる
- ステップ3. 過去問を解く
ステップ1. 基礎を理解する
数学を暗記するにも最低限の基礎理解は必要です。
例えば行列の問題を解くのに「行列同士の積」がわからなかったら問題を解くことすらできないですよね。
要は出題される分野の基礎的な教科書に書いてあることは理解しておけば大丈夫です。基礎理解ができたら何回も基礎を勉強する必要はありません。すぐに応用問題に進みましょう。冒頭でも話しましたが型1つから構成される問題しか出題されないので、一般入試の上位国公立大学を受験するような対策は不要です。
基礎数学のおすすめ参考書はありますか?
と聞かれることも多いのですが、高専で使用している教科書を使うのがいいですよ。
高専は編入試験のプロなので、高専で使われている教科書は編入試験と非常に相性がいいです。
z
僕も神戸大学を受験するのに高専の教科書を使用して基礎固めをしたのですがかなりわかりやすかったです。大学範囲の数学って難しい教科書しかなく嫌になりますけど、高専で使われている教科書はかなり噛み砕かれているのでおすすめです。
一般の人でも購入できるので基礎から数学を勉強するなら出題される分野に応じた教科書を使って勉強しましょう。
新基礎数学
数と式の計算、方程式と不等式、関数とグラフ、指数関数と対数関数、三角関数、図形と式、場合の数と数列
新線形代数
ベクトル、行列、行列式、行列の応用
新微分積分I
微分法、微分の応用、積分法、積分の応用
新微分積分Ⅱ
関数の展開、偏微分、重積分、微分方程式、微分方程式、関数の展開
新確率統計
確率、データの整理、確率分布、推定と検定
新応用数学
ベクトル解析、ラプラス変換、フーリエ解析、複素関数、微分方程式
ちなみに基礎数学を勉強する前に過去問分析をして志望校で出題される科目を把握して効率よく勉強する準備をしておきましょう。
詳しくは下記の記事を読んでみてください。
高専の参考書に抵抗がある人は、「編入数学徹底研究 頻出問題と過去問題の演習」の関連参考書がおすすめです。
こちらも「微分・積分」と「線形代数」に特化した2冊があります。
余談ですがこのことからも編入数学では、「微分・積分」と「線形代数」が重要であることがわかりますね。
編入の微分積分徹底研究
「編入数学徹底研究 頻出問題と過去問題の演習」でも十分丁寧に説明されていますが、基礎理解の部分が雑だったり、独学できない人はより詳しく解説しているこちらがおすすめ。
編入試験まで時間がじっくりあり、まだ微分・積分の基礎も怪しい人はぜひこの参考書で勉強して欲しいです。
編入の線形代数徹底研究
こちらも「編入数学徹底研究 頻出問題と過去問題の演習」で対応可能ですが、線形代数は基礎理解が難しかったりするので、やっておくと無難です。
これらの参考書は編入試験を受験する人向けの参考書なので、過去問でアウトプットできる章があったりとかなりおすすめです。
ステップ2. 「編入数学徹底研究」で問題に慣れる
基礎理解ができたらすぐに「編入数学徹底研究 頻出問題と過去問題の演習」に取りかかりましょう。
この参考書に出てくる問題が実際の受験で出題される問題です。
この参考書に出てくる問題を丸暗記すれば、ほぼ同じ問題しか出題されないので8割取れるようになります。
解答を見ながら進める
参考書の使い方ですがいきなり解答を見ながら進めればOK。
繰り返しますが編入数学はほぼ同じ問題しか出題されないので、初見で解ける必要は全くありません。
参考書で問題を解くときに、
へ〜!編入数学ってこんな問題形式なんだ。でも解き方わからないな…
と思ったらすぐに解答を見ましょう。
解答を見ながら1つ1つ理解しながら解き方を覚えておきます。ここで重要なのは疑問点を全てつぶすことです。
導出の過程がわからなかったりしてもうやむやにしていては駄目です。しっかり理解するのが重要です。
解答を読みながら進めたら、繰り返しましょう。2回、3回と繰り返すと解答を見なくとも解けるようになってきます。
こんなことして意味あるの?
と思うかもですが、ほぼ同じ問題しか出ませんし、応用と言ってもこの参考書で出ている問題の一部が変わった問題ばかりです。
暗記すれば数学は驚くほど解けるようになりますよ。
僕はこの方法で勉強を進めて、参考書に掲載されている問題がほぼ初見で解けませんでしたが神戸大学工学部の数学は自己採点ですが100点近く取れました。
ステップ3. 過去問を解く
参考書をある程度繰り返したら過去問に挑戦してみましょう。
例えばですが「神戸大学 工学部」を受験する方なら出題される分野が出題されている他大学の過去問も解くと幅が広がりますよ。
編入試験は過去問ベースで出題されるので過去問対策は必ずしておきたいです。
まとめ:編入数学の対策は簡単です
以上ですが、編入数学の対策方法がわかったかと思います。
文系学部受験で数学が苦手な方はこの方法で他受験生と差をつけることができるのでぜひ挑戦していただきたいです。また理系学部の方も数学を得点源とすれば合格に近づくかと思います。
大学編入試験は決して難しくありません。しっかり対策をたて、努力すれば国公立大学や難関私立大学に合格することが可能です。あなたも編入試験で人生を変えてみませんか?ステップ編入学院が全力でサポートさせていただきます。まずはお気軽にご相談ください。